多変量解析とは？マーケティングにおける目的や主な分析手法を解説！

統計解析手法である「多変量解析」は、企業のマーケティングの場でも活用されています。この記事では、多変量解析の意味や目的、具体的な手法を解説しています。
数学的な情報は省き、初学者でもなるべく理解しやすい内容になっているので、企業でデータ分析に携わる方は、ぜひ参考にしてみてください。

多変量解析とは

多変量解析とは、複数のデータ構造から知見を得たり、数値の予測を立てたりすることに優れている手法群です。特定の手法を指すものではなく、複数の手法を総称して「多変量解析」と呼びます。

多変量解析の名称にある「変量」とは、資料の調査項目や観測項目などです。例えば、次のように学校のテスト結果を一覧で示した時、「算数」「国語」の2つの調査項目が「変量」にあたります。

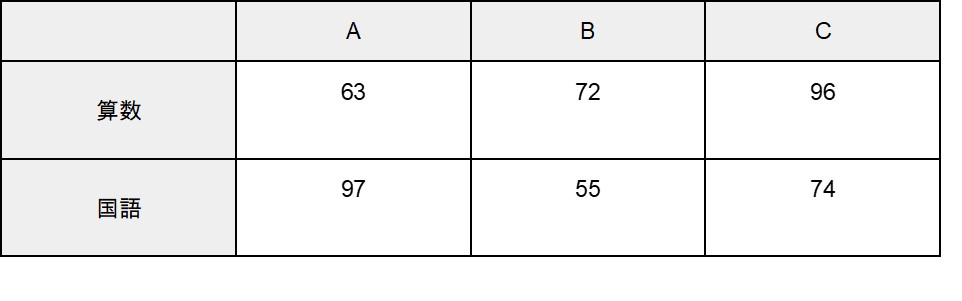
このとき、変量が複数（算数と国語）あるので、上記のデータを分析する手法の総称が「多変量解析」となります。一方で、変量が1つしかない（例えば算数だけ）場合、データを分析する手法は「単変量解析」といいます。

マーケティングにおける多変量解析の目的

多変量解析は心理学や経済、政治など多様な分野で適用されますが、企業のマーケティング実務でも用いられる統計解析手法です。多変量解析の目的は、大きく「予測」と「判別」の2つに分けられます。これら2つの目的において、どのような分析方法を用いるのか解説します。

販売数や購入有無などの予測・判別

多変量解析は、複数のデータから未来を予想する「予測」のために用いられます。例えば、予測の手法の1つである「重回帰分析」を使えば、新規出店の売上を席数や商圏人口などからある程度予想することが可能です。

なお、多変量解析の「予測」は、予想する対象によって、さらに次の2つに分類できます。

• 数値（量的データ）を予想する→予測
• カテゴリ（質的データ）を予想する→判別

「予測」も「判別」も予想することには変わりありませんが、多変量解析では上記のように使い分けることを理解しておきましょう。

データをわかりやすく分類する「要約」

人間は、膨大なデータとそのカテゴリを見たときに、頭の中で即座に整理することは困難です。仮にできたとしても、変量3個あたりまでが限界でしょう。多変量解析は、変量が多いデータをより少ない変量にまとめて理解しやすくする「要約」のために用いられます。

例えば、ドラッグストアやスーパーマーケットなどで、過去に購入された商品の売上や購入頻度などを比較するとしましょう。このとき、商品のカテゴリは多岐に渡るため、単純に比較することが難しくなります。

そこで、要約の手法の1つである主成分分析を用いて、膨大な商品を「食品」「日用品」などのようにカテゴリをまとめる（要約）することで、データを理解しやすくできるのです。
要約の多変量解析では、予測や判別などは行わず、外的基準なしにデータを分析します。

多変量解析で使われる用語の意味

多変量解析には、変量についていくつか専門用語が出てきます。多変量解析を知るうえで理解しておきたい4つの用語の意味を解説します。

量的データ・質的データ

変量には種類があり、大きく「量的データ」と「質的データ」の2つに分けられます。それぞれの意味を詳しく解説します。

量的データ

「量的データ」とは、数値で表されるデータを指します。マーケティングの場面においては、次のようなデータを量的データといいます。

• 売上
• 来店客数
• 購買量
• 年齢
• 家計支出　など

質的データ

量的データとは反対に、数値で表せないデータを「質的データ」といいます。マーケティングの場面においては、次のようなデータが該当します。

• 性別
• 国籍
• 血液型
• 既婚／未婚
• 購買理由　など

尺度

統計学において、データが持つ性質を分類するのが「尺度」です。尺度は、量的データに用いるか、質的データに用いるかで、次のように分類できます。

比率尺度

量的データの中でも、0に絶対的な意味を持つ尺度を「比率尺度」といいます。量的データの多くは、この比率尺度に分類されます。

「0に絶対的な意味を持つ」とは、すなわち「値が0になると何もない」という意味です。例えば、比率尺度に分類される「滞在時間」が0のとき、客が店舗などに「滞在していない」という状態を指します。一方で、気温は0℃であっても「気温がない」とはなりません。そのため、気温は後述する間隔尺度に分類されます。

比率尺度に分類される尺度は、滞在時間のほかにも次のようなものがあります。

• 売上
• 来店客数
• 購買量
• 購入単価　など

間隔尺度

比率尺度とは反対に、量的データの中でも0に相対的な意味を持ち、変数の差が意味を表す尺度を「間隔尺度」といいます。

例えば、間隔尺度に分類される「気温」は、10℃と30℃では20℃の差があることになります。気温は「差」に意味を持つため、30℃は10℃の3倍の暑さとはなりません。一方で、先ほど解説した比率尺度に分類される滞在時間は「1時間の3倍は3時間」が成り立ちます。

変数の差が意味を持つ間隔尺度は、気温以外にも次のようなものがあります。

• 西暦
• 偏差値
• 年齢　など

順序尺度

質的データにおいて、数値の大小や順序に意味を持つ尺度を「順序尺度」といいます。本来、質的データは数値にできないデータを指しますが、データを数値に置き換えることがあります。例えば「顧客の購買意欲」のような質的データも、次のように数値に置き換えることが可能です。

• 購入したい＝1
• どちらでもない＝0
• 興味がない＝－1

この時、数値が大きいほど、購買意欲が高いことがわかります。このように、数値の大小や順序に意味を持つ尺度が順序尺度です。マーケティングの場面においては、次のようなデータが該当します。

• 商品満足度（5段階評価の1、2…）
• ランキング（1位、2位…）
• 等級（1級、2級…）

なお、置き換えた数値自体に意味はありません。そのため、数値の差や平均には意味を持たない点に注意しましょう。

名義尺度

内容を区別・分類するために用いられる尺度を「名義尺度」といいます。例えば「顧客の居住地」のような質的データは、順序尺度と同様に、数値に置き換えて集計が可能でかつ、数値の順序や差などには意味を成しません。

• 東京都＝1
• 神奈川県＝2
• 千葉県＝3
• 埼玉県＝4

他にもマーケティングの場面においては、次のようなデータが該当します。

• 性別
• 国籍
• 血液型
• 電話番号　など

多変量解析の種類

多変量解析の手法は、説明変数と目的変数がそれぞれ量的データか質的データかによって分類できます。さらに、「予測（予測・判別）」と「要約」でカテゴリ分類すると、多変量解析の代表的な手法は次のように分けられます。

• 説明変数…結果の原因となる変数
• 目的変数…原因を受けて発生した結果となる変数

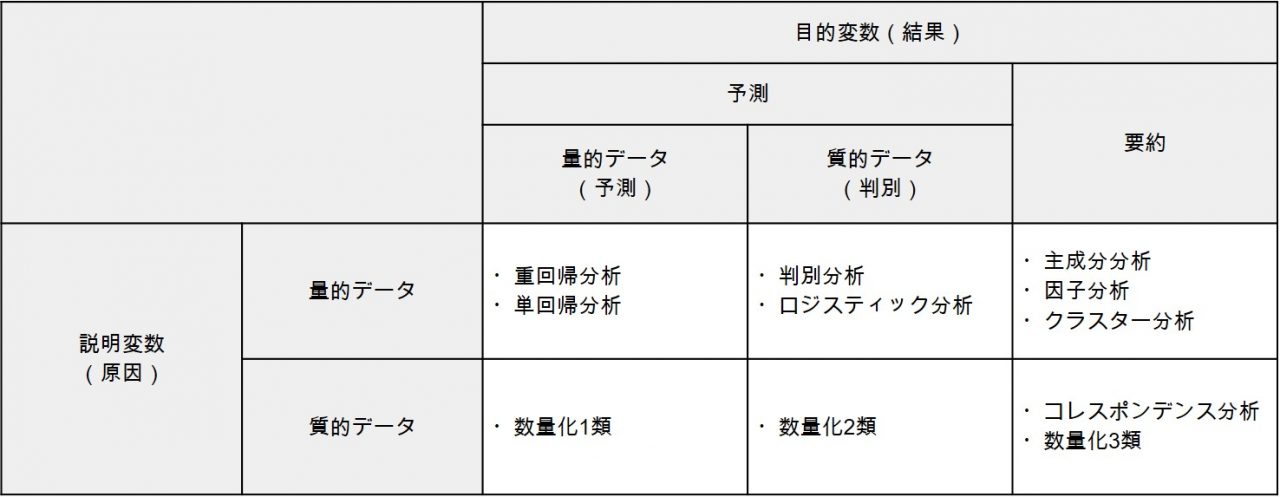
上記の表を参照すれば、「判別分析」は量的データ（説明変数）から質的データ（目的変数）を予測する手法だとわかります。

【予測】多変量解析の主な分析手法

予測に使われる多変量解析の代表的な手法を4つ解説します。

重回帰分析

重回帰分析とは、複数の説明変数から、1つの目的変数を予測しようとする手法です。量的データ（数値）から量的データ（数値）を予測する回帰分析のうち、説明変数が2つ以上となるのが重回帰分析です。なお、1つの説明変数から1つの目的変数を予測する回帰分析を「単回帰分析」と呼びます。
重回帰分析は、複数の変数から結果に対する要因の影響度を明らかにすることができます。

【企業の使用例】

• 取引額や商圏人口、店舗の席数などが、売上に対してどれほど影響しているか分析する
• 営業訪問件数や顧客満足度などが、取引額に与える影響を分析する

判別分析

判別分析とは、既存のデータ分布から、未知のデータがどのカテゴリに属するかを予測する手法です。量的データ（数値）から質的データ（カテゴリ）を予想します。

例えば、「体重と身長から性別を予測する」「検査データから症状を割り出す」といったように、過去に蓄積されたデータから「男性／女性」「症状あり／なし」といったカテゴリ区分が可能です。

判別分析は、在庫の発注や購入の有無を予測するなどの目的で使われます。数値データを膨大に蓄積している企業ほど、予測精度は高まります。

【企業の使用例】

• 在庫数や予定使用量などから、発注の有無を予測する
• 顧客の購入回数や購入頻度などから、リピートする顧客を割り出す

数量化１類

数量化1類とは、質的データ（カテゴリ）から量的データ（数値）を予想する手法です。質的データに数値を与えることで、目的変数である量的データを割り出します。

数量化とは、質的データを数値に置き換えることを指します。例えば「あなたの性別は何ですか？」という問いに対し、仮に男性なら1を、女性なら0を割り当てます（この0,1をダミー変数といいます）。説明変数である質的データを数値に変換することで、回帰分析が使えるため、カテゴリが数値に与える影響度を測ることが可能となります。

ビジネスの場では、性別や購買の有無などから購入単価や受注量などを予想するために、数量化1類を用いることが可能です。

【企業の使用例】

• 性別や職業、趣味などから購入単価を分析する
• 業種や季節などから、受注量を予測する

数量化２類

数量化2類とは、質的データ（カテゴリ）から質的データ（カテゴリ）を予想する手法です。数量化2類は判別分析とほぼ同じ手順で、説明変数と目的変数の質的データ（カテゴリ）を数値に変換することで、目的変数の質的データを分析します。

数量化1類では説明変数のみ質的データを数値に置き換えましたが、数量化2類では目的変数の質的データも数値に変換します。目的変数が質的データ（カテゴリ）となるため、原理としては判別分析と同じです。説明変数にも数値を割り当てることで、判別分析と同様、要因から分類される結果を予測します。

【企業の使用例】

• 性別や職業、趣味などから購入の有無を予測する
• 業種や季節などから、受注の有無を予測する

【要約】多変量解析の主な分析手法

要約に使われる多変量解析の代表的な手法を4つ解説します。

主成分分析(PCA)

主成分分析とは、多くの説明変数をまとめて、より数の少ない合成変数（主成分）を作り出す手法です。

企業に蓄積されたビッグデータは膨大な変量を含むため、それだけで分析するのは困難です。そこで、変量を人間が理解できる数まで分類し、データを理解しやすくしようとするのが主成分分析の目的です。

例えば、ある飲料会社の飲料製品5つの販売量を調整したいマーケティング担当者が、5段階の顧客満足度アンケート調査を元に主成分分析で解析するとしましょう。主成分分析の計算式は複雑なため、基本的に統計ソフトやPythonなどを使用します。今回はPythonを使って、架空のアンケート調査結果を次のように散布図として出してみました。

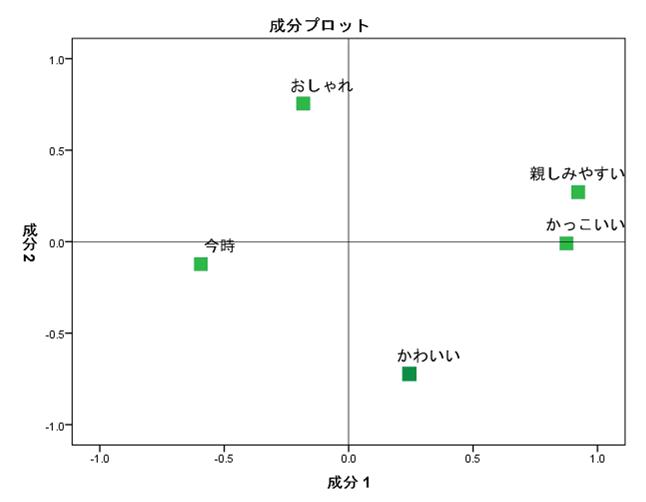
上記の散布図には主成分（「第1主成分」と「第2主成分」）が表示されていますが、統計ソフトやPythonなどを使うと、主成分が具体的に何を表すかまではわかりません。そのため、分析者自身が仮説を立てる必要があります。

まず、顧客満足度に最も貢献している第1主成分は、一般的に総合得点を指しています（上記散布図の横軸）。そして、縦軸の第2主成分は分析者自身が仮説を立てたうえで分析を行います。

仮に、横軸と縦軸の得点が高い飲料Bと飲料Eが、それぞれ「ジュース」と「乳飲料」だとしましょう。このとき、第2主成分を表す縦軸は2つの飲料に共通する「甘み」と仮説を立てられるため、甘い飲料の販売を伸ばすといった施策を検討できます。

このように主成分分析はアンケート調査結果を活かして施策を立案する際や、企業の研究開発などの場面で用いられる解析手法となっています。

因子分析

主成分分析と同様に、因子分析も多くの変量を要約することが目的の手法です。因子分析と主成分分析は、よく混同されることがあります。違いとしては、主成分分析は観測変数を統合する考え方であるのに対し、因子分析は観測変数に与える原因・条件を分析しようとする手法である点です。

例として、顧客が商品購入する際に重視している要因を明らかにするために、コスメを販売する会社が、顧客に対してアンケートを実施したとしましょう。

【設問】「コスメ商品を購入した決め手として、各項目で最も当てはまるものを選んでください」

• 気軽に相談できた
• ブランドが有名
• 店員の丁寧な接客
• SNSで見た
• CMで見た
• 商品展開が豊富
• 商品案内が親切
• 商品の質がいい
• 話題の商品だった

【回答】

• 当てはまる
• やや当てはまる
• どちらとも言えない
• やや当てはまらない
• 当てはまらない

上記の因子から、質問の因子（グループ）を作りつつ、次のように「寄与率」と「因子負荷量」を計算して表にします。今回、因子分析の結果によって、分析者は3つの因子を抽出しました。

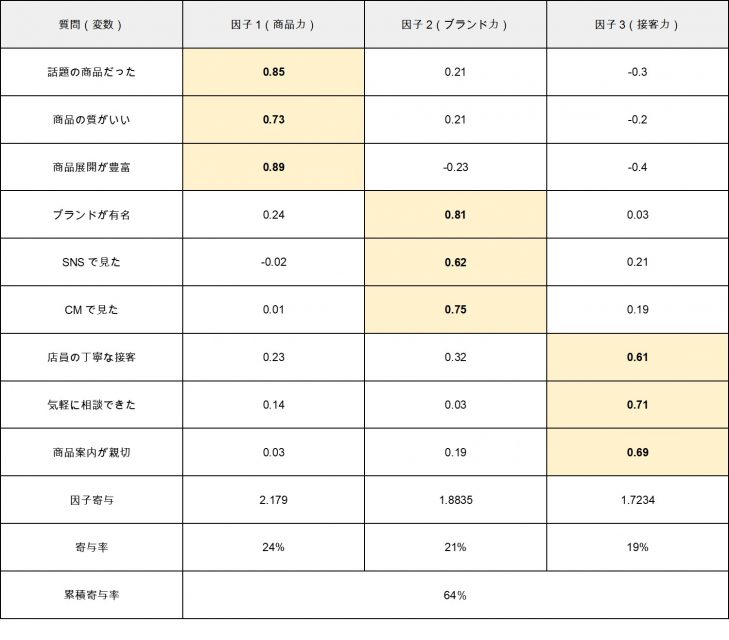
【用語解説】

• 因子負荷量…各因子に対し、変数がどれほど関与しているか表す数値。－1～+1の数値を取り、絶対値が大きいほど、共通因子と観測変数に強い相関（正または負）があることを示す。
• 因子寄与…因子が、すべての観測変数に対してどれほど影響しているか表す数値。因子負荷量の2乗和で求められる。
• 寄与率…各因子が、データ全体に対してどれほど寄与しているかを表す割合。
• 累積寄与率…寄与率を、大きい数値から順に足した数値。
  

因子1を見てみると、「話題の商品だった」「商品の質がいい」「商品展開が豊富」の因子負荷量が大きいことがわかります。そこで今回、分析者は因子1を「商品力」と定義しています。これら3つの質問（観測変数）が、商品力に寄与しやすいと推測できます。

また、上記の表では商品力の寄与率がもっとも高いので、今後「話題の商品だった」「商品の質がいい」「商品展開が豊富」に力を入れていくと、顧客満足度を底上げしやすいことが分析可能です。

このように因子分析は、アンケートの調査結果から潜在意識を明らかにしたり、変数（ここでは回答）間の関係性を解釈しやすかったりするメリットがあります。

クラスター分析

クラスター分析とは、異なる個々のデータから、似ているデータ同士をグルーピングする手法です。性質が似たクラスター（集団）を作ることで、外的基準のないデータをわかりやすく分類します。

クラスター分析は「階層クラスター分析」「非階層クラスター分析」の2つに分類できます。

• 階層クラスター分析…データ群の中から似ているデータを順番にまとめていき、いくつかのクラスターを作る手法。データ群をまとめる過程で樹形図（デンドログラム）ができる。
• 非階層クラスター分析…最終的なクラスター数を決め、似たもの同士をクラスターに割り当てる手法。ビッグデータのように、複雑な階層構造をしているデータに向いている。

例えば、飲食店で実施した顧客アンケートに階層クラスター分析を用いるとしましょう。

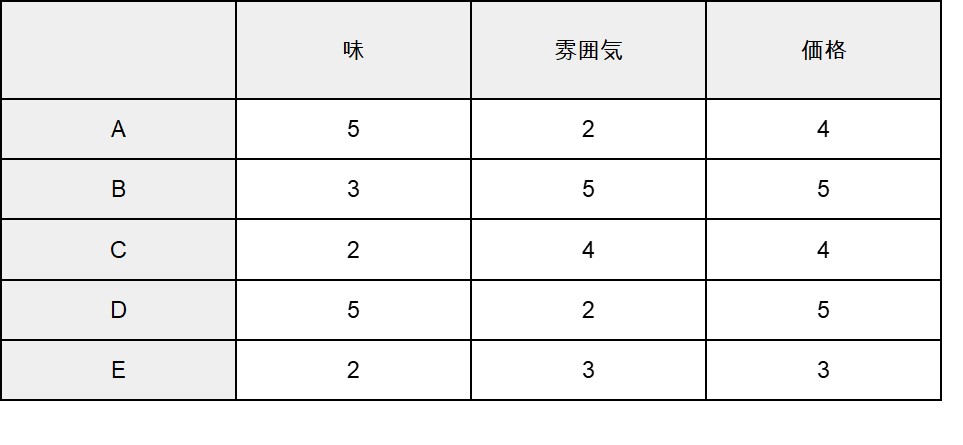
階層クラスター分析では、似ているものから順番にまとまり(クラスター)を表現している樹形図（デンドログラム）を用いることが多いです。

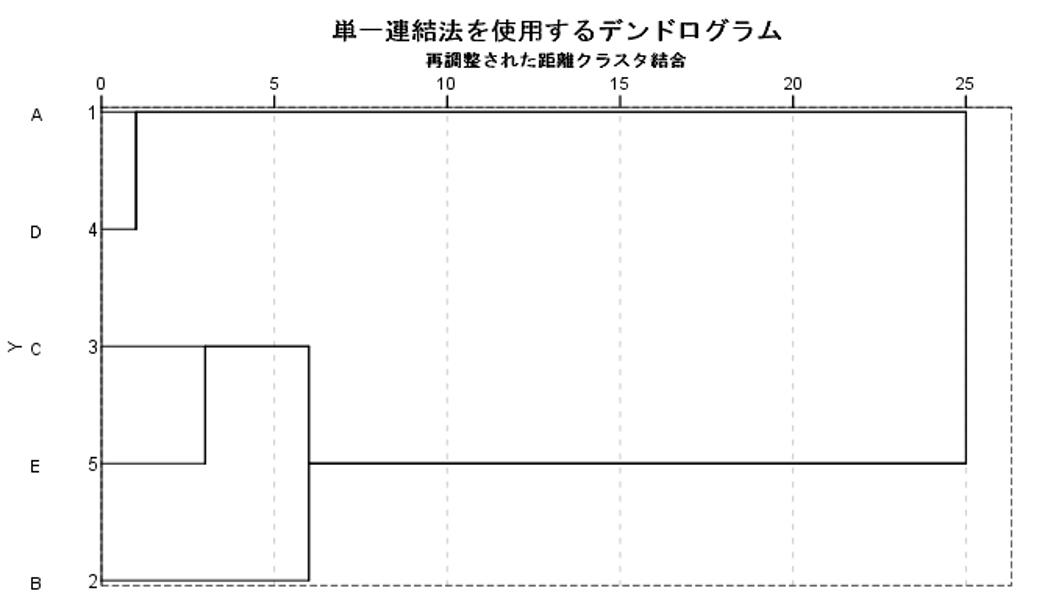
階層クラスター分析は、最初からクラスター数を決める必要がない利点がありますが、ビッグデータのようにデータ数が膨大な場合、樹形図が複雑な形になってしまいます。データ数が多くなる場合は、あらかじめクラスター数を決めてから分析する非階層クラスター手法が適しています。

コレスポンデンス分析

コレスポンデンス分析とは、多くのデータを散布図で表示し、わかりやすいようにデータを分類する手法です。コレスポンデンス分析の特徴として、質的データを取り扱うことにあります。

また、コレスポンデンス分析は、自社と競合のポジショニングを明確にすることに長けた手法です。例えば、飲料商品についての顧客アンケートを点数化した結果、次のようなデータを得られたとしましょう。

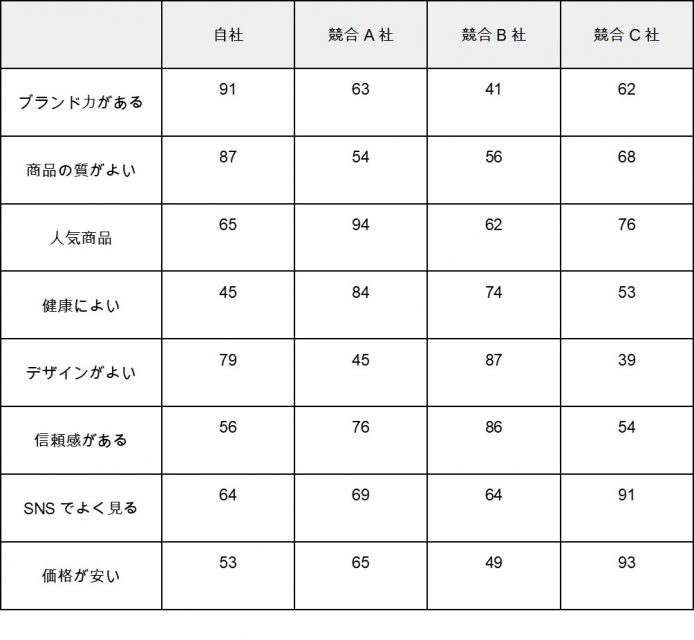
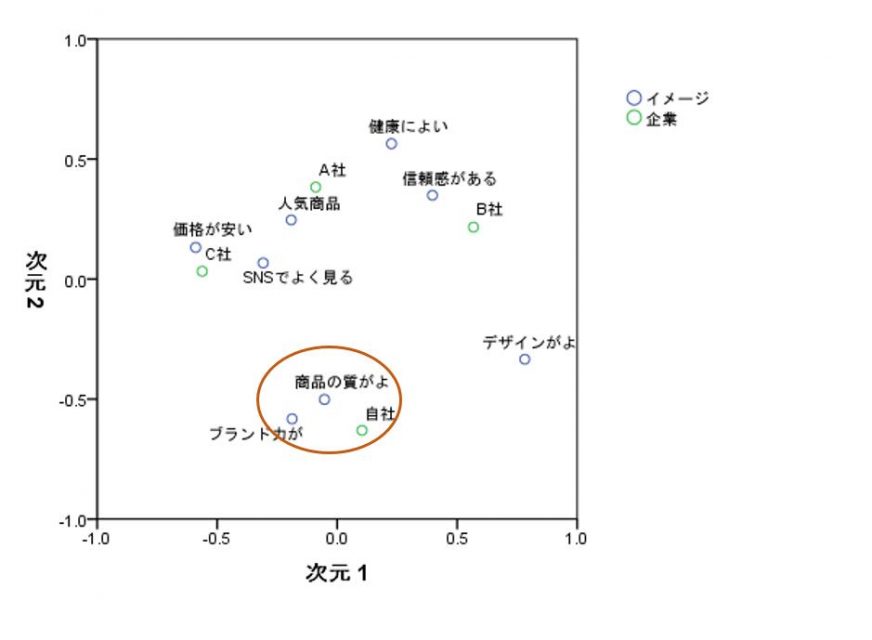
上記のように散布図を作成することで、類似度の高いカテゴリーや、軸の解釈などができます。例えば、上記の散布図を見てみると「ブランド力がある」と「商品の質がよい」は距離が近いので、深く関連しており、また自社はこの2点で競合に対して優位性を発揮できているとわかります。

まとめ：多変量解析は「予測」と「要約」のための手法

多変量解析は、複数のデータ構造から知見を得たり予測したりすることに優れた手法群です。多変量解析の手法は、データから未来を予想・判別する「予測」と、膨大なデータをまとめて理解しやすくする「要約」の2つに大きく分類できます。
ビッグデータを取り扱ううえで重要な統計解析手法なので、ぜひ理解しておきましょう。

本メディアを運営するマーケティング・リサーチ・サービスは、市場調査や顧客分析のほかにも、自社内の既存データ分析を強みとした会社です。企業に蓄積された膨大な情報を分析することは、先鋭的な商品開発や正確な売上予測を立てることにもつながります。自社内に蓄積されたデータを活用したい企業様は、ぜひマーケティング・リサーチ・サービスまでお問い合わせください。